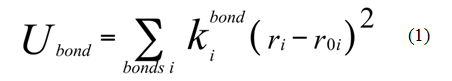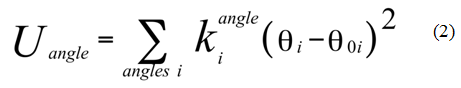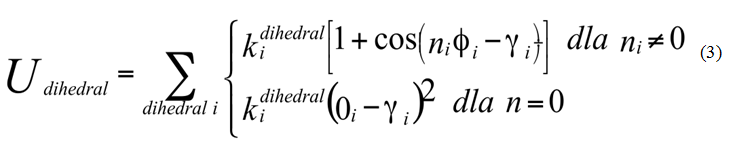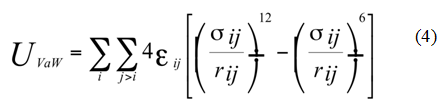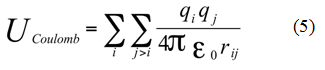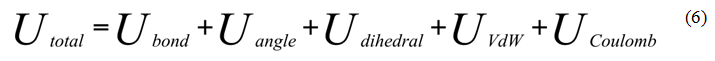Pole siłowe CHARMM

Pole siłowe CHARMM

Pole siłowe opisuje oddziaływania między atomami za pomocą prostych funkcji matematycznych, których wartość można w miarę szybko obliczyć. Wartości parametrów z tych funkcji są wynikiem długiej i żmudnej procedury iteracyjnej, polegającej na dopasowywaniu tych parametrów do wyników obliczeń kwantowo mechanicznych i danych doświadczalnych, takich jak długości wiązań, kąty między wiązaniami, ciepło właściwe, względne równowagi między konformerami związków, częstości drgań. W polu siłowym CHARMM (opis równań w pracy [16]), tak jak we wszystkich polach siłowych, cząsteczka traktowana jest jako układ kulek połączonych sprężynkami, a energia potencjalna opisana jest poprzez wielkości geometryczne i wraz z odpowiednimi parametrami.

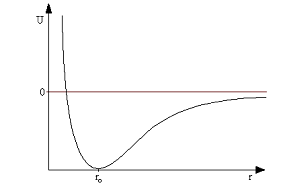
Funkcja opisująca zmiany energii potencjalnej dwu atomów w zależności od wzajemnej odległości ich jąder ma kształt krzywej Morse'a (Rys. 2).

Rysunek 2. Krzywa Morse’a, gdzie r oznacza odległość między dwoma atomami połączonymi wiązaniem chemicznym, a U jest energią potencjalną tego układu.

Z przedstawionego wykresu widać, że minimum energii potencjalnej przypada na odległość r0. Wiązanie chemiczne większości molekuł ma skończoną odległość, umiejscowioną w pobliżu r0. Dlatego poszukując energii potencjalnej danego wiązania, zamiast rozwiązywać skomplikowane wyrażenie na krzywą Morse’a, możemy w zakresie bliskich odległości od r0 uprościć funkcję potencjału stosując prawo Hooke’a (równanie 1):

gdzie kibond oznacza stałą siłową rozciągania wiązania, a r0i wartość równowagową długości tego wiązania.

Kolejnym parametrem jest potencjał zginania kąta pomiędzy dwoma wiązaniami tego samego atomu. Jest on opisywany również przez funkcję 2-go stopnia (równanie 2):

Energia potencjalna rośnie gdy wartość kąta θ oddala się od wartości kąta θ0. kiangle oznacza stałą siłową zginania kąta pomiędzy dwoma wiązaniami, natomiast θ0i równowagową wartość tego kąta.

Kiedy cząsteczka składa się z większej liczby atomów do jej opisu potrzebny jest jeszcze człon torsyjny, gdyż nie sposób określić barier rotacyjnych (np.: w etanie) posługując się tylko energią rozciągania wiązań i zginania. W polu siłowym CHARMM energia torsyjna opisana jest następująco (równanie 3):

gdzie i jest kątem torsyjnym (dwuściennym), a i kątem fazowym.

Wyrażenie na całkowitą energię potencjalną powinno również uwzględniać oddziaływania dalekozasięgowe. Do najczęściej uwzględnianych oddziaływań należy: oddziaływanie van der Waalsa i oddziaływanie elektrostatyczne. W polu CHARMM oddziaływania van der Waalsa wyrażone zostały poprzez potencjał Lennarda-Jonesa:

gdzie σij jest wielkością stałą.

Oddziaływanie elektrostatyczne jest opisane klasycznym równaniem Coulomba:

gdzie qi, qj to ładunki cząstkowe na atomach i oraz j, a ε0 przenikalność elektryczna.

Kiedy uwzględnimy wszystkie typy oddziaływań otrzymamy wyrażenie pozwalające wyznaczyć całkowitą energię potencjalną badanego układu:

Dla pola siłowego CHARMM [5, 6, 17-19] całkowita energia potencjalna (Utotal) jest sumą energii pochodzących od poszczególnych członów, czyli odpowiednio od energii wiązań (Ubond), od energii kątów płaskich (Uangle), od energii kątów dwuściennych (Udihedral) oraz od energii oddziaływań van der Waalsa (UVdW) i elektrostatycznych (UCoulomb).

Trzeba jednak zaznaczyć, że wartość energii całkowitej cząsteczki, jest jedynie energią steryczną zależną od użytej parametryzacji pola siłowego i jej bezwzględna wartość jest niefizyczna.

Literatura

1. Ponder, J. W., and Case, D. A. (2003) Force fields for protein simulations. Adv Protein Chem 66, 27-85.
2. Cheatham, T. E., 3rd, and Young, M. A. (2000) Molecular dynamics simulation of nucleic acids: successes, limitations, and promise. Biopolymers 56, 232-56.
3. Cornell, W. D., Cieplak, P., Bayly, C. I., Gould, I. R., Merz, K. M. Jr., Ferguson, D. M. Spellmeyer, D. C., Fox, T., Caldwell, and J. W., Kollman, P. A. . (1995) A second generation force field for the simulation of proteins, nucleic acids and organic molecules. J. Am. Chem. Soc. 117, 5179-5197.
4. Pearlman, D. A., Case, D. A., Caldwell, J. C., Seibel, G. L., Singh, U. C., Weiner, P., & Kollman, P. A.,. (1991) AMBER 4.0. University of California, San Francisco.
5. MacKerell, A. D., Bashford, D., Bellott, M., Dunbrack, R. L., Evanseck, J. D., Field, M. J., Fischer, S., Gao, J., Guo, H., Ha, S., Joseph-McCarthy, D., Kuchnir, L., Kuczera, K., Lau, F. T. K., Mattos, C., Michnick, S., Ngo, T., Nguyen, D. T., Prodhom, B., Reiher, W. E., Roux, B., Schlenkrich, M., Smith, J. C., Stote, R., Straub, J., Watanabe, M., Wiorkiewicz-Kuczera, J., Yin, D., and Karplus, M. (1998) All-atom empirical potential for molecular modeling and dynamics studies of proteins. Journal of Physical Chemistry B 102, 3586-3616.
6. MacKerell, A. D., Wiorkiewicz-Kuczera, J., and Karplus, M. (1995) An all-atom empirical energy function for the simulation of nucleic acids. Journal of the American Chemical Society 117, 11946-11975.
7. Pavelites, J. J., Bash, P. A., Gao, J., and MacKerell, A. D. (1997) A Molecular Mechanics Force Field for NAD+, NADH, and the Pyrophosphate Groups of Nucleotides. Journal of Computational Chemistry 18, 221-239.
8. Hermans, J., Berendsen, H. J. C., van Gunsteren, W. F., and Postma, J. P. M.,. (1984) A Consistent Empirical Potential for Water-Protein Interactions. Biopolymers 23, 1.
9. Ott, K.-H., B. Meyer. (1996) Parametrization of GROMOS force field for oligosaccharides and assessment of efficiency of molecular dynamics simulations. J Comp. Chem. 17, 1068-1084.
10. (1994), Biosym Technologies, San Diego.
11. Clark, M., Cramer III, R. D., and van Opdenhosch, N. (1989) Validation of the General Purpose Tripose 5.2 Force Field. J. Comp. Chem. 10, 982-1012.
12. Levitt, M., and Lifson, S. (1969) Refinement of protein conformations using a macromolecular energy minimization procedure Journal of Molecular Biology 46, 269-279.
13. Gunsteren, W. F., and Karplus, M. J. (1980) A method for constrained energy minimization of macromolecules. Journal of Computational Chemistry 1, 266-274.
14. Fletcher, R., and Reeves, C. M. (1964) Function minimization by conjugate gradients. The Computer Journal 7, 149-154.
15. Fletcher, R. (1980) Practical Methods of Optimization, Vol. 1, John Wiley & Sons, New York.
16. Phillips, J. C., Braun, R., Wang, W., Gumbart, J., Tajkhorshid, E., Villa, E., Chipot, C., Skeel, R. D., Kale, L., and Schulten, K. (2005) Scalable molecular dynamics with NAMD. J Comput Chem 26, 1781-802.
17. Nilsson, L., and Karplus, M. (1986) Empirical Energy Functions for Energy Minimizations and Dynamics of Nucleic Acids. Journal of Computational Chemistry 7, 591-616.
18. MacKerell, A. D., Feig, M., and Brooks, C. L. (2004) Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. Journal of Computational Chemistry 25, 1400-1415.
19. Feller, S. E., and MacKerell, A. D. (2000) An Improved Empirical Potential Energy Function for Molecular Simulations of Phospholipids. Journal of Physical Chemistry B 104, 7510-7515.