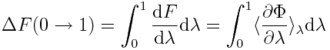Energia swobodna (projektowanie leków)

Energia swobodna (projektowanie leków)

Wiązanie białko-ligand - często modelowany pierwszy etap komputerowo-wspomaganego projektowania leków - wydaje się być prostym zjawiskiem asocjacji dwóch cząsteczek. Ważne jest, aby zdać sobie sprawę dlaczego nie jesteśmy jeszcze w stanie "projektować" leków tak jak mosty czy samochody. We wszystkich tych przypadkach (projektowanie leków, mosty, samochody), opis fizyczny jest znany. Niestety, dokładność wymagana przy obliczaniu energii swobodnej wiązania liganda jest zaskakująco wysoka - co najmniej 1 kcal/mol (choć właściwie dokładność poniżej 0,5 kcal/mol odpowiadałaby dokładności eksperymentalnej, a zatem - być może - wymaganej przez biologię). Taka dokładność, o ile w ogóle możliwa, jest ekstremalnie trudna do uzyskania. Gdyby udało się odnaleźć metodę o takiej dokładności, bylibyśmy świadkami rewolucji w projektowaniu leków.

Jednakże dokładność nie jest jedynym celem motod wyznaczania energii swobodnej. Drugim ważnym celem jest koszt obliczeniowy. Poszukując potencjalnych inhibitorów pośród 100000 cząsteczek nie możemy sobie pozwolić na obliczenia trwające nawet 1 godzinę/ligand. Tu stajemy przed problemem: czy doskonalić dokładność metod wyznaczania energii swobodnej? Czy poświęcić dokładność na rzecz przeszukiwania większych zbiorów potencjalnych leków?

Błąd przy generowaniu miniatury: /bin/bash: /usr/bin/convert: No such file or directory GPL Ghostscript 8.70: Unrecoverable error, exit code 1

Rys. 1.: Cykl termodynamiczny dla wiązania ligandu (L) przez białko (P). Ligand w roztworze (L) może mieć inną konformację, niż ligand związany z białkiem (L'). Pionowe przejścia odpowiadają wiązaniu liganda, zaś poziome transformacji L w L'. Energię swobodną wiązania można wyliczyć niezależnie od wybranej drogi, w konsekwencji: ΔF1+ΔF3=ΔF4+ΔF2.

W tym artykule przedstawimy kilka przykładów zastosowania metod wyznaczania energii swobodnej. Wszystkie opisać można jako "niekowalencyjne wiązanie dwóch biocząsteczek". Rys. 1. przedstawia konstrukcję cyklu termodynamicznego często wykorzystywanego w tego typu problemach. W zależności od przejść zmiany energii swobodnej są łatwiej, bądź trudniej wyznaczane. (Słowo "łatwy" oznacza tutaj: dający lepszą dokładność przy niższych nakładach obliczeniowych.) Każdy przykład zawiera odniesienia do prac, które stanowią dobry wstęp do danej tematyki.

Wiązanie białko-ligand

Ogólne zasady wykorzystywane przy analizie wiązań białko-ligand znaleźć można w [1]. W wielu przypadkach koncentrujemy się na różnicach energi swobodnej wiązania między zestawem ligandów i/lub białek-mutantów. Podobnie jak w eksperymencie, metody komputerowe potrzebują ścisłej definicji odwracalnej przemiany między stanem początkowym i końcowym. Zmiany energii swobodnej w przejściach poziomych na Rys. 1. można wyznaczyć, przykładowo, wykorzystując całkowanie termodynamiczne (TI):

gdzie energia potencjalna, Φ, zależy od parametru λ, a nawiasy kątowe oznaczają uśrednianie po zespole odpowiadającym Φ(λ), tzn. po konfiguracjach uzyskanych z symulacji z wykorzystaniem Φ(λ). Różnice w energii swobodnej wiązania można też uzyskać z transformacji poziomych (Rys. 1.), jednakże tego typu symulacje byłyby bardziej kosztowne obliczeniowo i trudniejsze do skonstruowania. Ale niezależnie od metody i wybranej drogi, metody obliczniowe pozwalają szacować różnice energii swobodnej.

Metody komputerowe mają jednak dwie podstawowe wady. Po pierwsze, są - trzeba przyznać - dość zawiłe (o czym świadczyć mogą chociażby artykuły w tym wiki), wymagają wiedzy eksperckiej i dużego doświadczenia. Po drugie, nie interesują nas tylko stany końcowe (ligand związany / ligand wolny), ale faktyczna ścieżka łącząca te dwa stany. Aby wiedzieć którędy wiedzie droga, musimy zapostulować coś o wielowymiarowej przestrzeni konfiguracyjnej generowanej przez badany układ. Tu pojawia się ryzyko narzucenia niewydajnego, bądź (co gosza) błędnego mechanizmu przejścia.

Dobre podsumowanie metod stosowanych w problemie wiązania białko-ligand znaleźć można w [2,3,4].

Zwijanie i stabilność białek

Literatura

1. Ligand-preceptor interactions, Comput. Chem. (1984), 8, 281--283. B. Tembe, J.A. McCammon.
2. Frontiers in free-energy calculations of biological systems, WIREs Comput Mol Sci. (2014), 4, 71--89, C. Chipot.
3. Standard Binding Free Energies from Computer Simulations: What is the Best Strategy, J. Chem. Theory Comput. (2012), 9, 794--802.
4. Free energy calculations of protein-ligand interactions, Current opinion in chemical biology (2011), 15.4, 547--552.