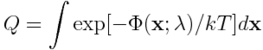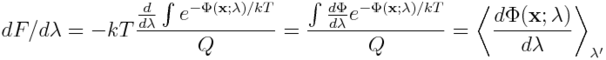(Utworzył nową stronę „=Thermodynamic Integration (TI)= '''Do dokończenia na 10. marca'''”) |
(→Thermodynamic Integration (TI)) |
||
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
=Thermodynamic Integration (TI)= | =Thermodynamic Integration (TI)= | ||
| − | ''' | + | Popularna metoda wyznaczania różnic energii swobodnej między układami o zbliżonych funkcjach energii potencjalnej. |
| + | TI powstała na gruncie podejścia perturbacyjnego ([[Free Energy Perturbation (FEP)|FEP]]), ale pozwala wyznaczać bardziej ogólne własności układu (potencjał średnich sił, PMF), aniżeli samą różnicę energii swobodnej. | ||
| + | Podstawową zaletą TI jest prostota; wyniki można interpretować bez rozbudowanej wiedzy fizycznej, zaś potencjalne źródła błędów w wynikach łatwo jest zlokalizować. | ||
| + | |||
| + | Najbardziej oczywistą wadą TI jest konieczność wyznaczania pochodnej potencjału Φ po parametrze porządku λ. | ||
| + | Im większy spadek PMFa (wyższa wartość pochodnej) tym gęściej powinny być rozmieszczone wartości λ, dla których przeprowadzane zostaną symulacje. | ||
| + | Bez uprzedniej znajomości kształtu PMFa trudno jest ocenić, jak powinno przebiegać całkowanie. | ||
| + | |||
| + | ==Formalizm== | ||
| + | Wychodząc z poniższej definicji energii swobodnej, | ||
| + | [[Image:F.png|thumb|center|x40px]] | ||
| + | gdzie ''Q'' jest całką po przestrzeni konfiguracyjnej: | ||
| + | [[Image:Q.png|thumb|center|x50px]] | ||
| + | podstawowe równanie TI otrzymujemy biorąc pochodną obydwu stron pierwszego równania: | ||
| + | [[Image:Dfdlambda.png|thumb|center|x60px]] | ||
| + | Oznacza to, że chcąc wyznaczyć zmiany energii swobodnej przeprowadzamy symulację przy potencjale Φ('''x''';λ), wyliczając średnią wartość pochodnej potencjału Φ po parametrze porządku λ. | ||
| + | Podejście naiwne polagałoby na wyliczeniu pochodnych energii swobodnej w równo rozmieszczonych punktach całkowania λ', a następnie na scałkowaniu zmierzonych wartości. | ||
| + | Jednak w rzeczywistości, punkty całkowania powinny być rozmieszczone gęściej w miejscach, w których energia swobodna zmienia się gwałtowniej. | ||
| + | Rozwiązanie tego problemu polega na wstępnym oszacowaniu kształtu PMFa i wyznaczeniu optymalnego rozmieszczenia punktów całkowania. | ||
| + | |||
| + | Bardziej subtelne problemy pojawiają się, gdy schodzimy z wartością parametru λ do wartości granicznych (zazwyczaj są nimi 0 i 1), gdy następuje "pojawianie się" (kreacja), bądź "znikanie" (anihilacja) atomów. | ||
| + | Wartości pochodnej energii swobodnej gwałtownie zmieniają się w tych punktach, co wymagałoby niezwykle gęsto rozmieszczonych punktów całkowania. | ||
| + | Jest kilka rozwiązań tego problemu, zainteresowanego czytelnika odsyłamy do [1]. | ||
| + | |||
| + | ==Literatura== | ||
| + | # ''Free energy calculations.'' Springer-Verlag Berlin Heidelberg (2007), C. Chipot , A. Pohorille. | ||
Aktualna wersja na dzień 13:09, 9 mar 2015
Thermodynamic Integration (TI)
Popularna metoda wyznaczania różnic energii swobodnej między układami o zbliżonych funkcjach energii potencjalnej. TI powstała na gruncie podejścia perturbacyjnego (FEP), ale pozwala wyznaczać bardziej ogólne własności układu (potencjał średnich sił, PMF), aniżeli samą różnicę energii swobodnej. Podstawową zaletą TI jest prostota; wyniki można interpretować bez rozbudowanej wiedzy fizycznej, zaś potencjalne źródła błędów w wynikach łatwo jest zlokalizować.
Najbardziej oczywistą wadą TI jest konieczność wyznaczania pochodnej potencjału Φ po parametrze porządku λ. Im większy spadek PMFa (wyższa wartość pochodnej) tym gęściej powinny być rozmieszczone wartości λ, dla których przeprowadzane zostaną symulacje. Bez uprzedniej znajomości kształtu PMFa trudno jest ocenić, jak powinno przebiegać całkowanie.
Formalizm
Wychodząc z poniższej definicji energii swobodnej,
gdzie Q jest całką po przestrzeni konfiguracyjnej:
podstawowe równanie TI otrzymujemy biorąc pochodną obydwu stron pierwszego równania:
Oznacza to, że chcąc wyznaczyć zmiany energii swobodnej przeprowadzamy symulację przy potencjale Φ(x;λ), wyliczając średnią wartość pochodnej potencjału Φ po parametrze porządku λ. Podejście naiwne polagałoby na wyliczeniu pochodnych energii swobodnej w równo rozmieszczonych punktach całkowania λ', a następnie na scałkowaniu zmierzonych wartości. Jednak w rzeczywistości, punkty całkowania powinny być rozmieszczone gęściej w miejscach, w których energia swobodna zmienia się gwałtowniej. Rozwiązanie tego problemu polega na wstępnym oszacowaniu kształtu PMFa i wyznaczeniu optymalnego rozmieszczenia punktów całkowania.
Bardziej subtelne problemy pojawiają się, gdy schodzimy z wartością parametru λ do wartości granicznych (zazwyczaj są nimi 0 i 1), gdy następuje "pojawianie się" (kreacja), bądź "znikanie" (anihilacja) atomów. Wartości pochodnej energii swobodnej gwałtownie zmieniają się w tych punktach, co wymagałoby niezwykle gęsto rozmieszczonych punktów całkowania. Jest kilka rozwiązań tego problemu, zainteresowanego czytelnika odsyłamy do [1].
Literatura
- Free energy calculations. Springer-Verlag Berlin Heidelberg (2007), C. Chipot , A. Pohorille.