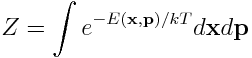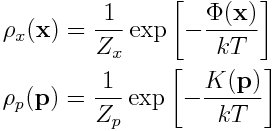(→Energia swobodna) |
(→Energia swobodna) |
||
| Linia 18: | Linia 18: | ||
[[Image:Boltzmann.png|thumb|center ]] | [[Image:Boltzmann.png|thumb|center ]] | ||
zwanej rozkładem Boltzmanna. | zwanej rozkładem Boltzmanna. | ||
| − | Stała ''k'' występująca w powyższych równaniach nosi nazwę stałej Boltzmanna. | + | Stała ''k'' występująca w powyższych równaniach nosi nazwę stałej Boltzmanna, natomiast stała ''Z'' jest stałą normalizacyjną: |
| + | [[Image:Z.png|thumb|center ]] | ||
| + | |||
Ludwig Boltzmann, twórca jednego z najważniejszych działów fizyki - mechaniki statystycznej - zasłużył się, proponując następującą postać funkcyjną entropii: | Ludwig Boltzmann, twórca jednego z najważniejszych działów fizyki - mechaniki statystycznej - zasłużył się, proponując następującą postać funkcyjną entropii: | ||
| Linia 28: | Linia 30: | ||
Energia swobodna ma bardzo prostą interpretację probabilistyczną, która bezpośrednio łączy się z naszymi intuicjami związanymi z wieloma zjawiskami molekularnymi (wiązanie ligandów przez enzymy, praca pomp transmembranowych, asocjacja białek itd.). | Energia swobodna ma bardzo prostą interpretację probabilistyczną, która bezpośrednio łączy się z naszymi intuicjami związanymi z wieloma zjawiskami molekularnymi (wiązanie ligandów przez enzymy, praca pomp transmembranowych, asocjacja białek itd.). | ||
Jednakże aby do tej "prostej interpretacji probabilistycznej" dojść, potrzebujemy zaobserwować kilka własności energii swobodnej. | Jednakże aby do tej "prostej interpretacji probabilistycznej" dojść, potrzebujemy zaobserwować kilka własności energii swobodnej. | ||
| − | Dokładne wyprowadzenia znaleźć można w [1]. | + | Dokładne wyprowadzenia znaleźć można w [1,2]. |
| + | |||
| + | # Rozkład prawdopodobieństwa położeń, '''x''', jest niezależny od rozkładu prowdopodobieństwa pędów, '''p'''. | ||
| + | To znaczy, rozkład Boltzmanna zapisać można jako: | ||
| + | [[Image:Rho.png|thumb|center ]] | ||
| + | gdzie | ||
| + | [[Image:Rhoxrhop.png|thumb|center ]] | ||
| + | |||
| + | |||
| + | # Równanie na energię swobodną można zapisać w postaci | ||
| Linia 35: | Linia 46: | ||
===Literatura=== | ===Literatura=== | ||
| − | # ''Molecular Modelling: Principles and Applications (2nd Edition)'', A. Leach | + | # ''Molecular Modelling: Principles and Applications (2nd Edition)'', A. Leach. |
| + | # ''Understanding Molecular Simulation (2nd Edition): From Algorithms to Applications'', D. Frenkel. | ||
Wersja z 11:52, 9 lut 2015
Spis treści
Energia swobodna
Energia swobodna jest wielkością fizyczną przydatną w opisie układów, będących w kontakcie z otoczeniem (tzn. oddziaływujących z nim). Pojęcie to wywodzi się z termodynamiki fenomenologicznej, gdzie służyło m.in. do określenia maksymalnej pracy, jaką można uzyskać ze zgromadzonej w układzie energii (stąd określenie swobodna), przy określonym typie oddziaływań z otoczeniem (termiczne, mechaniczne, materialne). Jednakże energia swobodna (i jej pochodne cząstkowe) pozwala wyznaczyć wszystkie makroskopowe równowagowe własności układu.
Zarys historyczny
W zestawie artykułów Energia swobodna, które znaleźć można w ramach tego wiki, ograniczamy sie do opisu energii swobodnej Helmholtza:
czyli potencjału termodynamicznego stosowanego w przypadku układów w kontakcie termicznym z otoczeniem (przy stałej liczbie cząsteczek, N, i stałej objętości, V). Energia swobodna Helmholtza w powyższej postaci ograniczona jest do układów makroskopowych, tzn. zbudowanych z niewyobrażalnie dużej liczby cząsteczek. Należy podkreślić, że termodynamika fenomenologiczna nie zakłada, że otaczająca nas materia zbudowana jest z atomów, a jedynie postuluje istnienie i właściwości dwóch funkcji: energii wewnętrznej (U) i entropii (S).
Postać mikroskopowa energii swobodnej
Ponieważ zajmujemy się układami w skali mikro (białka, kwasy nukleinowe itd.), interesować nas będzie postać energii swobodnej Helmholtza, wynikająca z postulatów mechaniki statystycznej. To znaczy,
gdzie w miejsce energii wewnętrzenej pojawiła się wartość oczekiwana energii całkowitej, E, przy gęstości prawdopodobieństwa:
zwanej rozkładem Boltzmanna. Stała k występująca w powyższych równaniach nosi nazwę stałej Boltzmanna, natomiast stała Z jest stałą normalizacyjną:
Ludwig Boltzmann, twórca jednego z najważniejszych działów fizyki - mechaniki statystycznej - zasłużył się, proponując następującą postać funkcyjną entropii:
Zauważmy, że do wyznaczenia energii swobodnej potrzebna jest znajomość energii całkowitej układu, która jest funkcją położeń, x, i pędów atomów, p, z których zbudowany jest układ.
Dlaczego energia swobodna jest taka ważna?
Energia swobodna ma bardzo prostą interpretację probabilistyczną, która bezpośrednio łączy się z naszymi intuicjami związanymi z wieloma zjawiskami molekularnymi (wiązanie ligandów przez enzymy, praca pomp transmembranowych, asocjacja białek itd.). Jednakże aby do tej "prostej interpretacji probabilistycznej" dojść, potrzebujemy zaobserwować kilka własności energii swobodnej. Dokładne wyprowadzenia znaleźć można w [1,2].
- Rozkład prawdopodobieństwa położeń, x, jest niezależny od rozkładu prowdopodobieństwa pędów, p.
To znaczy, rozkład Boltzmanna zapisać można jako:
gdzie
- Równanie na energię swobodną można zapisać w postaci
Literatura
- Molecular Modelling: Principles and Applications (2nd Edition), A. Leach.
- Understanding Molecular Simulation (2nd Edition): From Algorithms to Applications, D. Frenkel.